原文链接（国家基金委网站）：http://www.nsfc.gov.cn/publish/portal0/tab448/info79101.htm

在国家自然科学基金项目（批准号：61633014、61573221、61873332、61922051）资助下，beat365手机官方网站张焕水和徐娟娟研究团队在线性二次最优控制的研究方面取得进展。最新研究成果以“时滞正倒向随机差分方程的解及其应用（Solution to Delayed Forward and Backward Stochastic Difference Equations and Its Applications）”为题，于2020年5月21日在《IEEE自动控制汇刊》（IEEE Transactions on Automatic Control, IEEE TAC）上在线发表。论文链接：https://ieeexplore.ieee.org/document/9097877。

线性二次最优控制（LQR）是现代控制理论的基本问题之一，在经济和自动化等领域具有重要应用。LQR的根本问题可归结为一组正倒向微分/差分方程（FBDEs）的求解，对于标准LQR问题，FBDEs的解可由标准Riccati（黎卡提）方程给出，从而获得最优控制器。然而对于复杂的LQR，FBDEs求解仍面临挑战，由此LQR一些重要基础问题有待解决，如上个世纪60年代末提出的非正则LQR问题（也称“Singular Control”问题），其可解条件以及与传统LQR的本质区别长期困扰人们；再如时滞系统随机LQR问题，虽然随机控制的基本问题在上世纪七十年代已得到解决，但是时滞情形下的随机LQR长期面临挑战，Smith预估器控制理论也因此无法应用于乘性噪声随机系统。由于这些问题未得到根本性解决，从而直接或间接地阻碍了其他相关控制问题研究，包括丢包/延迟下网络控制系统的反馈镇定、信息非对称最优控制等。

该团队在深入研究传统方法的基础上，通过提出新的一般FBDEs解耦求解方法发展了传统最优控制方法，取得了系列成果。通过将时滞系统随机控制的复杂性归结为时滞随机FBDEs解耦求解问题，得到了与传统LQR结果平行一致的结论并包含已有结果作为特例[IEEE TAC, 2017, 62(1): 350-365]；通过求解非正则FBDEs，揭示了非正则LQR与标准（正则）LQR的本质区别并给出了问题可解的充要条件[SCIENCE CHINA Information Science, 2019, 62(9): 192203]。这些问题的解决标志着LQR控制理论日趋完善，随机控制已能够延伸至时滞情形以及Smith预估控制器被推广至乘性噪声随机系统。在此基础上，该团队提出了网络控制系统在丢包和传输时滞同时发生情形下反馈镇定的充要条件，得到了平均场随机系统反馈镇定的充要条件[IEEE TAC, 2019, 64(3): 1125-1136]以及信息非对称网络控制系统的最优控制[Automatica, 2018, 98: 86-94]。

在此基础上，该团队进一步研究了一类更一般的时滞随机FBDEs，通过提出新型Riccati差分方程，建立了倒向随机过程与正向随机过程及其条件期望之间的非齐次关系，得到了一般时滞随机FBDEs的显式解。进而将多输入时滞随机LQR问题转化为一般时滞随机FBDEs，利用得到的FBDEs解析解给出了多输入时滞随机LQR问题的显式最优控制器。

该团队提出的一般FBDEs解耦求解方法是对传统控制方法的进一步完善，弥补了传统方法面临复杂控制问题的不足，推动了LQR控制理论的发展，为智能机器人/无人车跟踪控制等实际控制系统性能的提升提供有效理论方法和技术手段。

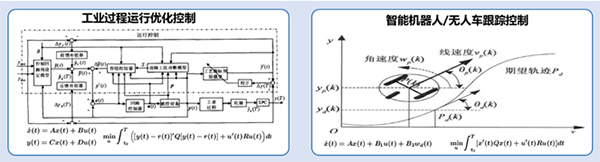
图 线性二次最优控制的应用